چگونه محاسبه ضریب همبستگی
در تحلیل دادهها، یکی از مهمترین مسائل درک ارتباط بین متغیرها است. برای اینکه بتوانیم این ارتباط را بهطور دقیقتری ارزیابی کنیم، نیاز به معیارهایی داریم که نشان دهند آیا تغییرات یک متغیر با تغییرات متغیر دیگر ارتباط دارد یا خیر. یکی از این معیارها، ضریب همبستگی است که در بسیاری از زمینهها، از جمله آمار، اقتصاد و علوم اجتماعی، بهکار میرود.
ضریب همبستگی معیاری است که نشان میدهد تا چه اندازه دو متغیر با هم ارتباط دارند و این ارتباط به چه صورت است. به عبارت دیگر، این ضریب مشخص میکند که تغییرات در یک متغیر تا چه حد میتوانند تغییرات در متغیر دیگر را پیشبینی کنند. محاسبه صحیح این ضریب میتواند اطلاعات ارزشمندی درباره نحوه تعامل دادهها فراهم کند.
در این مقاله، مراحل و روشهای مختلف محاسبه ضریب همبستگی بررسی خواهد شد. بهویژه، تمرکز بر روی نحوه انجام محاسبات بهصورت گامبهگام و کاربردهای آن در تحلیلهای مختلف خواهد بود. درک دقیق این مفاهیم میتواند به تحلیلگران کمک کند تا از دادهها بهطور مؤثرتری استفاده کنند.
مفهوم ضریب همبستگی در آمار
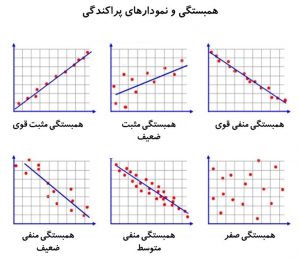
در آمار، یکی از اهداف اصلی تحلیل دادهها شناسایی و سنجش روابط بین متغیرها است. ارتباط میان دادهها میتواند بهصورت مثبت، منفی یا حتی بدون ارتباط باشد. این ارتباطات میتوانند نقش مهمی در پیشبینی و تحلیل روندها ایفا کنند. برای اندازهگیری شدت و نوع این ارتباطات، از مفهومی به نام ضریب همبستگی استفاده میشود. این ضریب به تحلیلگران کمک میکند تا ارتباط بین دو مجموعه داده را بهطور کمی ارزیابی کنند.
تعریف ضریب همبستگی
ضریب همبستگی یک عدد است که میزان ارتباط بین دو متغیر را نشان میدهد. این عدد معمولاً بین -1 و 1 قرار دارد. اگر ضریب همبستگی برابر 1 باشد، نشاندهنده ارتباط کاملاً مثبت است؛ به این معنی که افزایش یا کاهش یکی از متغیرها بهطور مستقیم و با شدت معادل بر دیگری تأثیر میگذارد. اگر ضریب همبستگی برابر -1 باشد، ارتباط بین متغیرها منفی و کاملاً معکوس است. مقدار صفر نشاندهنده عدم وجود هیچگونه ارتباط خطی است.
انواع ضریب همبستگی
ضریب همبستگی میتواند در انواع مختلفی محاسبه شود. از جمله معمولترین آنها میتوان به ضریب همبستگی پیرسون و ضریب همبستگی اسپیرمن اشاره کرد. ضریب همبستگی پیرسون بیشتر برای دادههای پیوسته و خطی مناسب است، در حالی که ضریب همبستگی اسپیرمن برای دادههای رتبهای و غیرخطی کاربرد دارد.
| ضریب همبستگی | نوع ارتباط | محدوده مقدار |
|---|---|---|
| ضریب همبستگی پیرسون | خطی و پیوسته | -1 تا 1 |
| ضریب همبستگی اسپیرمن | غیرخطی و رتبهای | -1 تا 1 |
درک مفهوم ضریب همبستگی به تحلیلگران این امکان را میدهد که روابط میان دادهها را بهتر درک کرده و از آنها برای پیشبینی روندهای آینده یا بررسی مدلهای مختلف استفاده کنند. این ابزار بهویژه در تحلیلهای اقتصادی، پزشکی، و اجتماعی اهمیت زیادی دارد.
چگونه ضریب همبستگی را محاسبه کنیم؟
محاسبه ضریب همبستگی بهعنوان یک فرآیند ریاضی نیازمند شناخت روشهای خاص و انجام محاسبات دقیق است. این محاسبات بهطور معمول شامل مقایسه مقادیر مختلف دو متغیر و ارزیابی نحوه ارتباط آنها با استفاده از فرمولها و الگوریتمهای خاص میباشد. در این بخش، مراحل گامبهگام محاسبه ضریب همبستگی را بررسی خواهیم کرد.
مراحل محاسبه ضریب همبستگی
برای محاسبه ضریب همبستگی معمولاً از روشهای مختلفی استفاده میشود. در اینجا، مراحل پایهای محاسبه ضریب همبستگی پیرسون آورده شده است:
- جمعآوری دادهها: ابتدا باید دو مجموعه داده از متغیرهای موردنظر جمعآوری شود.
- محاسبه میانگینها: برای هر مجموعه داده، میانگین مقادیر آن محاسبه میشود.
- محاسبه تفاضلها: تفاوت هر مقدار از میانگین مربوطه محاسبه میشود.
- ضرب تفاضلها: تفاضلهای محاسبهشده برای هر جفت داده با یکدیگر ضرب میشوند.
- جمع نتایج ضربشده: تمام ضربهای حاصلشده جمع میشوند.
- محاسبه انحرافات معیار: برای هر مجموعه داده، انحراف معیار محاسبه میشود.
- محاسبه ضریب همبستگی: در نهایت، ضریب همبستگی با استفاده از فرمول خاص محاسبه میشود.
فرمول محاسبه ضریب همبستگی پیرسون
فرمول ضریب همبستگی پیرسون بهصورت زیر است:
r = Σ((xi - μx) * (yi - μy)) / (√Σ(xi - μx)² * Σ(yi - μy)²)
در این فرمول:
- r: ضریب همبستگی پیرسون
- xi و yi: مقادیر متغیرهای x و y
- μx و μy: میانگینهای متغیرهای x و y
- Σ: جمع مقادیر
با استفاده از این فرمول میتوان ارتباط میان دو متغیر را بهصورت عددی ارزیابی کرده و شدت و نوع این ارتباط را مشخص کرد.
انواع ضریب همبستگی و کاربردهای آن
ضریب همبستگی بهعنوان یک ابزار تحلیلی، انواع مختلفی دارد که هرکدام برای تحلیل روابط خاص بین دادهها و متغیرها طراحی شدهاند. انتخاب نوع ضریب همبستگی بستگی به ویژگیهای دادهها و هدف تحلیل دارد. هر نوع ضریب همبستگی کاربردهای خاص خود را در زمینههای مختلف علمی و تحقیقاتی دارد.
در این بخش به معرفی چند نوع پرکاربرد از ضریب همبستگی و کاربردهای آنها در تحلیل دادهها خواهیم پرداخت. این ضریبها نهتنها در آمار بلکه در بسیاری از علوم دیگر، مانند اقتصاد، پزشکی، روانشناسی و مهندسی، کاربرد دارند.
ضریب همبستگی پیرسون
ضریب همبستگی پیرسون یکی از رایجترین انواع ضریب همبستگی است که برای اندازهگیری ارتباط خطی میان دو متغیر پیوسته استفاده میشود. این ضریب معمولاً برای دادههایی که دارای توزیع نرمال هستند، مناسب است و مقادیر آن بین -1 و 1 قرار دارد. مقدار 1 نشاندهنده ارتباط کامل مثبت، -1 نشاندهنده ارتباط کامل منفی و 0 نشاندهنده عدم وجود ارتباط خطی است.
کاربردها: این نوع ضریب همبستگی در تحلیلهای آماری و مدلسازی دادهها در زمینههایی مانند تحلیل بازار بورس، پیشبینی روندهای اقتصادی، و تحلیل تأثیر متغیرهای محیطی بر سلامت انسانها بسیار کاربرد دارد.
ضریب همبستگی اسپیرمن

ضریب همبستگی اسپیرمن برای اندازهگیری رابطه میان دو متغیر رتبهای یا دادههای غیرخطی استفاده میشود. این ضریب بیشتر در شرایطی کاربرد دارد که دادهها خطی نباشند یا توزیع نرمال نداشته باشند. برخلاف ضریب پیرسون، ضریب اسپیرمن بر اساس رتبهها محاسبه میشود و برای دادههایی با مقیاس رتبهای یا دادههایی که روابط پیچیدهتری دارند، مناسب است.
کاربردها: این ضریب در تحقیقات روانشناسی، جامعهشناسی، و تحلیلهای پزشکی برای بررسی روابط غیرخطی بین ویژگیهای مختلف، مانند ارتباط بین رتبهبندی افراد در گروههای مختلف یا تأثیر عوامل غیرقابل اندازهگیری بر یک متغیر، مورد استفاده قرار میگیرد.
ضریب همبستگی کندال
ضریب همبستگی کندال مشابه ضریب اسپیرمن است و برای بررسی روابط رتبهای بین دادهها استفاده میشود. این ضریب بیشتر در مواردی که دادهها دارای نوسانات زیاد یا مقیاسهای مختلف هستند کاربرد دارد. کندال معمولاً برای تحلیل دادههایی با حجم کوچکتر یا روابط پیچیدهتر بهکار میرود.
کاربردها: این ضریب در تحقیقات جغرافیایی، علوم اجتماعی و پیشبینی الگوهای طبیعی مورد استفاده قرار میگیرد. همچنین در مواردی که دادهها حاوی اطلاعات پراکنده و غیرمرتبط هستند، میتواند مفید باشد.
در نهایت، انتخاب نوع ضریب همبستگی بستگی به ویژگیهای دادهها و هدف تحلیل دارد. استفاده صحیح از هرکدام از این ضریبها میتواند بهطور چشمگیری دقت تحلیلها و پیشبینیها را افزایش دهد.
تأثیر اندازه دادهها بر ضریب همبستگی
اندازه دادهها یکی از عوامل مهمی است که میتواند تأثیر زیادی بر محاسبه ضریب همبستگی داشته باشد. در واقع، تعداد نمونهها و ویژگیهای توزیع دادهها نقش تعیینکنندهای در دقت و صحت نتایج محاسبات دارند. هرچه دادهها بیشتر و متنوعتر باشند، نتایج ضریب همبستگی معمولاً دقیقتر و قابلاعتمادتر خواهند بود. از سوی دیگر، استفاده از دادههای کمحجم یا نمونههای نادرست میتواند منجر به نتایج گمراهکننده شود.
تأثیر اندازه دادهها بر ضریب همبستگی به این صورت است که با افزایش تعداد دادهها، معمولاً احتمال وقوع نوسانات تصادفی کمتر شده و رابطه واقعی میان متغیرها بهطور واضحتری نمایان میشود. در مقابل، با کاهش تعداد دادهها، ضریب همبستگی ممکن است بهطور غیرمنتظرهای تغییر کند و از ارتباط واقعی دور شود.
علاوه بر این، اندازه دادهها میتواند بر شدت و نوع ارتباط بین متغیرها نیز تأثیر بگذارد. در نمونههای کوچک، ممکن است ضریب همبستگی نشاندهنده یک ارتباط قوی بهنظر برسد، در حالی که در صورت افزایش اندازه دادهها، این ارتباط ضعیفتر یا حتی غیرخطی به نظر برسد. بنابراین، در تحلیلهای آماری، توجه به تعداد نمونهها و ویژگیهای آنها از اهمیت بالایی برخوردار است.
در نهایت، برای دستیابی به نتایج معتبر و دقیق در محاسبه ضریب همبستگی، باید دقت کافی در انتخاب اندازه نمونهها و نوع دادهها بهکار برده شود. انتخاب نمونههای بزرگ و متنوع، همراه با بررسی ویژگیهای دادهها، میتواند به تحلیلگران کمک کند تا از ضریب همبستگی بهعنوان یک ابزار مؤثر در تحلیل روابط استفاده کنند.
ضریب همبستگی در تحلیل دادهها
ضریب همبستگی یکی از ابزارهای کلیدی در تحلیل دادهها است که به تحلیلگران کمک میکند تا روابط میان متغیرها را شناسایی و بررسی کنند. این ابزار نهتنها برای تحلیلهای آماری بلکه برای پیشبینی روندها و تصمیمگیری در حوزههای مختلف علمی و تجاری نیز کاربرد دارد. در واقع، ضریب همبستگی بهعنوان یک شاخص کمی، میتواند نشان دهد که تغییرات یک متغیر چگونه بر تغییرات متغیر دیگر تأثیر میگذارد.
در تحلیل دادهها، یکی از مهمترین چالشها شناسایی نوع و شدت ارتباط بین متغیرها است. ضریب همبستگی این امکان را فراهم میآورد که ارتباط خطی یا غیرخطی میان دادهها را بهطور دقیق اندازهگیری کرده و به تحلیلگر اطلاعات مفیدی در خصوص الگوهای پنهان دادهها ارائه دهد. این ابزار بهویژه زمانی مفید است که بخواهیم روابط پیچیده میان چندین متغیر را بررسی کنیم.
استفاده از ضریب همبستگی در تحلیلهای دادهای میتواند به شفافسازی بسیاری از پرسشهای تحقیقاتی کمک کند. بهعنوان مثال، در تحقیقات علمی، این ضریب میتواند نشاندهنده تأثیرات متقابل بین متغیرهای مختلف، مانند ارتباط میان مصرف کالای خاص و درآمد مصرفکنندگان، یا ارتباط بین میزان تحصیلات و سطح سلامت فردی باشد.
در نهایت، ضریب همبستگی در تحلیل دادهها ابزاری است که میتواند به تصمیمگیرندگان کمک کند تا مدلهای دقیقتری از روابط موجود میان متغیرها بسازند و از آنها برای پیشبینی و برنامهریزی استفاده کنند.